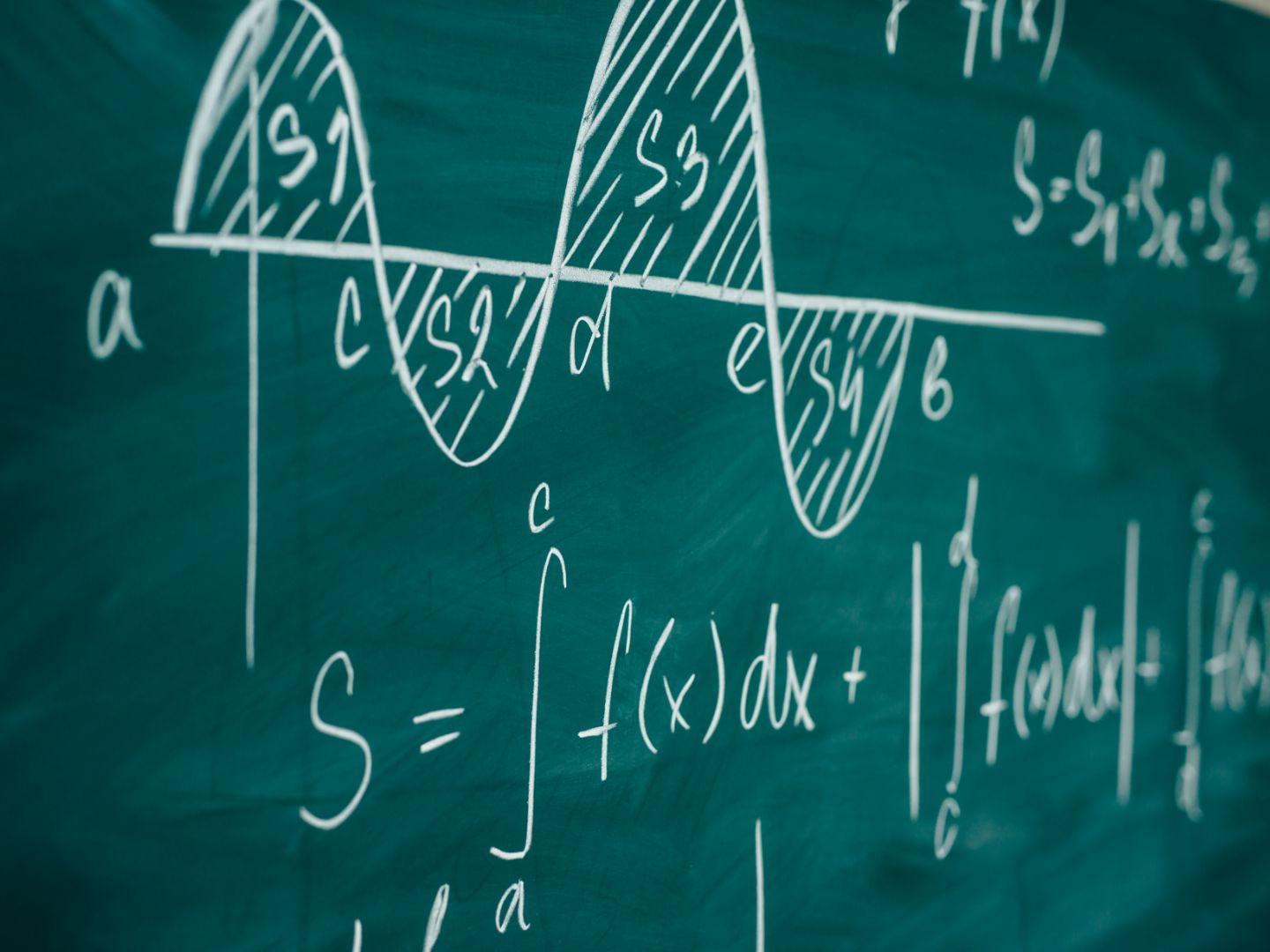How to get better at math in 7 simple steps

This post will teach you how to get better at math faster and with less studying. You’ll still have to study, but it tells you the right things to focus on.

A common issue with most people is that they think math skills are innate. They believe that either you get math or you don’t.

In high school, I had this issue as well. I figured that I didn’t get the math gene and ,because of this, there was no chance of me doing anything in my future that required crunching numbers, writing computer programs, or science.

According to psychology, I was a victim of a fixed mindset. I simply didn’t think I could actually get better at math. Or at the very least, I wasn’t willing to sacrifice the time and energy necessary to get my math grade and number skills up.

I was one of those students who actually took pride in my lack of math skills. I avoided challenging myself with more difficult and interesting math and science courses. Beyond what was mandatory, I only took biology so that I could avoid math-heavy physics and chemistry courses

If I couldn’t rely on memorization to get through the class, I didn’t want to study it.

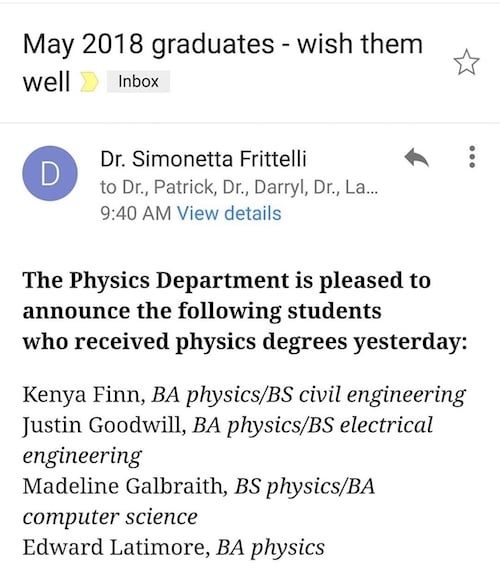
I ordered my high school transcripts to look at my math grades. As you can see, I was not.

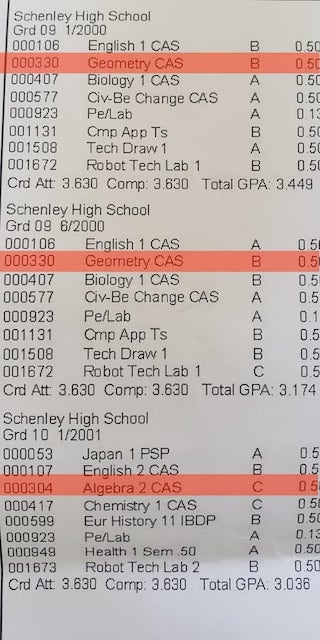
It should come as no surprise that I struggled in high school to get even a C in my high school math courses

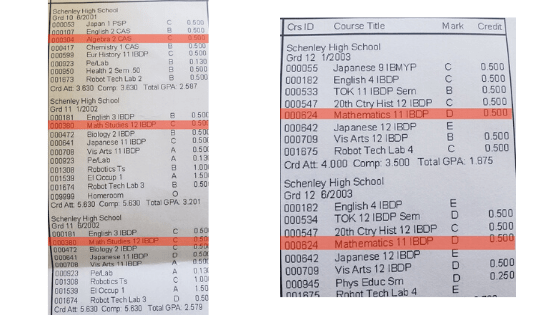
Even when I graduated in 2003, I figured that it didn’t make sense to get a degree in anything that didn’t require learning math. So I tried again. This time, my failure would cause me to fail out of college in my third semester in 2004.

Fast forward 14 years to 2018.

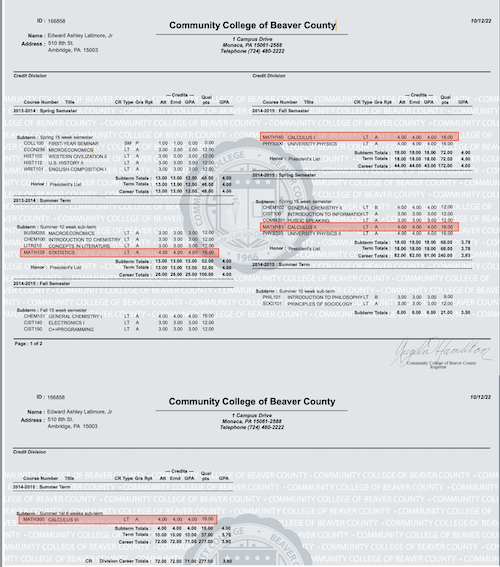
At the age of 33, I not only graduated from Duquesne University with a B.A. in Physics and a minor in Mathematics, but I was also making $1000 per week as a tutor for high school students in physics, chemistry, and math.

Academically, I didn’t get lower than a B in any of my math classes. Professionally, I was doing such a great job as a tutor that I had a new issue: I had to turn down business. So the question is how did I do it??

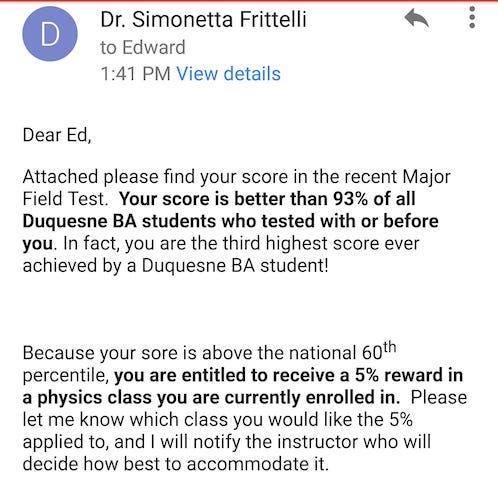
What did I do to finally handle my issues with math?

How did I go from being a mediocre student in high school who could barely get basic math concepts to earning a degree that’s so math intensive that you automatically get a math minor by completing it?

How did I go from someone who was terrified of trigonometry and doing derivatives to someone who got several high school students through AP Calculus and AP Physics?

This article details the simple step-by-step method I used to handle my issues with basic arithmetic, help me to understand higher-level calculus, and be able to do every level of math in between.

This article will take your abilities to the next level if you want to get better at math. You’ll feel more confident when you solve problems with numbers.

1) Believe that you can get it

If you’re like the typical student, you don’t think your brain can understand the concepts. You simply don’t think you can do it.

This is the single biggest issue you’ll face. That’s why it’s the first step to improving your math skills. You have to sincerely believe that you can learn math.

Most people who have an issue with math have simply convinced themselves that they can’t get it. They believe that they just weren’t born with a mind for math. I know this not only from observation, but from personal experience as well.

This is not a helpful mindset for learning.

I used to think the same thing about myself. I would rationalize my lack of ability by telling people I’m great at memorizing, but figuring out math wasn’t my thing. However, two things eventually changed my mind.

A) You’re likely at least as smart as the typical math student

Despite the fact that the average IQ of mathematics majors is higher, the average SAT score of someone who studies math is a bit more modest.

The average SAT score of a math major–someone who devotes four years to studying math–is only 1238 (out of 1600).

If that sounds high, I’ve tutored students to even higher SAT scores who started out in the sub-1000 range. Even if the future math majors score higher on the math section (which makes perfect sense), these findings suggest that overall, they aren’t any more intelligent than most people who go to college.

When I saw this, I figured that I could understand this subject.

B) Growth mindset comes from you achievements in other areas

Another thing that gave me confidence that I could get math was my experience in boxing.

I started boxing at the late age of 22. However, despite this late start, I went on to have a very successful career and overcame many issues throughout the process of becoming a boxer. At first, boxing may seem unrelated to improving at math, but I did not start boxing with any natural talent.

I worked hard, paid my dues, and watched myself go from a stumbling amateur to a national champion. My mentality with boxing was that I was going to succeed, no matter what.

When I went back to college in my late 20s, I took the same approach with my work. I figured that if I could succeed in boxing with a late start, then this would be easy.

These two events were extremely helpful in shifting my mindset. They showed me that there was nothing inherently special about people with decent math skills. At the very least, if I was smart enough to be accepted into college, then I was smart enough for numbers.

I also saw that I did one challenging thing by working hard. Think about other areas in your life where you’ve met challenges but didn’t have any initial talent or advantage. You probably had to work hard to make up for lost ground.

This will give you confidence in yourself.

2) Take your learning into your own hands

If you’re like me, you were educated in a public school system.

You had limited/non-existent resources for improving your math ability outside of the classroom. If you got a bad explanation or had to endure a subpar math teacher, there was no place you could go for help.

Of course, a big problem is that when I was in high school, there were nearly as much help available online. Fortunately, that’s no longer the case.

There are a plethora of free/low-cost materials online that are very good and extremely helpful. If your teacher isn’t getting the job done, learn on your own.

Here are a short list of ways to study math:

• Youtube videos
• Khan Academy
• Download problem sets solutions
• Download pdfs of textbooks
• For more problems, buy more used textbooks and study guides

You’ll need resources to improve your understanding. There’s no way around that. You’ll need to work on many practice problems to grasp many basic concepts. Fortunately, there is a solution on the internet for almost any problem somewhere. You can check if both your process and solution are correct.

Take advantage of all of the free resources on the internet. You need to practice math to improve at math.

If the explanations in class aren’t helping you get things, then there are great Youtube channels and websites out there that are excellent at explaining ideas.

3) Master the fundamentals of numbers and arithmetic

Now that you’re armed with the proper mindset and know how to acquire resources to practice with let’s lay out a good plan to increase your understanding.

When most people use the word “arithmetic”, they just mean working with numbers and general mathematics. They aren’t incorrect, but that’s too general for our purposes. In this case, I’m using arithmetic to mean the four basic operations you perform on numbers.

Those operations are addition, subtraction, multiplication, and division. These are the basic arithmetic operations.

These are the basic building blocks of all mathematics. They are present in all levels of math and permeate your daily life in many seemingly non-mathematical situations.

Many of us think we understand them but have problems adding negative numbers, quickly multiplying double-digit numbers, or working with fractions.

Here is a list of basic arithmetic skills students of math should master:

• Performing the basic arithmetic operations on negative numbers. These problems aren’t difficult, per se, but they tend to trip up our intuition about numbers.
• Performing the basic arithmetic operations on fractions. These problems tend to give people fits and halt their journey before it even begins. This intuition will also help you out with measuring and money problems.
• Quickly being able to multiply one or two-digit numbers by other two-digit numbers. You can solve these problems with calculators, but it does nothing to develop your numerical intuition.
• Quickly estimate how many times one number can be divided into another. These problems are the kind you’ll most encounter in the real world. You don’t need to compute the exact number (that’s definitely for calculators). A ballpark figure will often suffice.

The goal isn’t to be a human calculator that can perform amazing feats of mental calculation. Machines are faster, and at this point, it looks like you’ll always have access to a calculator (I’m old enough to remember when they used to tell us that we wouldn’t always have a calculator).

You want a level of comfort when working with numbers. This is necessary for words because we always speak, write, text, and type. With numbers, you have to develop a feel and fluency with them. Arithmetic practice is a good way to achieve this.

[A working level of basic math is one of the 12 major reasons why learning math is important. For the other 11 reasons, check out this article on why you should learn math.]

4) Hot tip: It’s all simple when you can read it

3 simple steps will help you read math and understand it better.

Step 1: The symbols and their meaning

You have to know that “¾” means “divide 3 into 4 equal parts. You have to know the difference between “ -3 + 0” and “3 - 0”. This might seem obvious, but I’ve found that many people lack mathematical aptitude due to not knowing basic stuff like this.

Make sure you know the symbols. You should not have to think about what it means to see |-4|. You may not know the answer, but you have to make sure that you at least know what it’s asking you.

Step 2: Synonyms of the symbols

The essence of math is how one thing is always exchangeable for another. In this way, we can make problems easier to work with.

“5/7” is the same thing is “5 *(1/7)”. Depending on your problem, one form may make more sense to use than another. This doesn’t just work for the numbers as well. You can swipe mine here if you don’t have a problem-solving process.

Learn different ways to express the same idea. For example:

• Adding a negative number is the same thing as subtracting its positive equivalent.
• Multiplication is the same thing as adding the same amount as many times you’re multiplying it.
• Dividing a fraction by a number is the same as multiplying by that number’s inverse.

These are just little examples of learning how to look at math as an interchange of ideas.

Some versions of ideas are easier to work with than others. Sometimes, we just need a different perspective to help us realize that we understand what’s going on.

Step 3: How the symbols work together

I could have simply titled this “The Order of Operations” section. That would cover most of what this section says and sort out most of the issues you have when it comes to learning math.

In case you forgot, the order of operations is as follows:

1. Parenthesis
2. Exponents
3. Multiplication
4. Division
5. Addition
6. Subtraction

We usually learn this with the mnemonic “Please Excuse My Dear Aunt Sally”. If you grasp nothing else in your math career, I recommend you learn this and its implications.

5) Little discussed tip: Think in pictures to solve problems

A big breakthrough in learning math was realizing that everything could be represented with a simple picture. The entire branch of geometry (and, to a lesser extent, trigonometry) relies on visual representation to teach its concept.

Taking a piece of paper to sketch can give you new ideas on old topics.

A few key visual representations are extremely helpful to know because they’re so common. You should familiarize yourself with them to improve your math skills.

A) The Number Line

This seems simple, but if you understand the number line, you have a visual model for every arithmetic operation possible. You’ll understand why multiplying two negatives gives you a positive, why you can’t take the square root of a negative number, and why we need imaginary numbers.

B) The Cartesian Plane

The real benefit of the Cartesian Plane is that it trains you to see relationships between things.

Specifically, how one quantity changes based on how another one changes. Algebra gives a lot of people fits because the addition of letters to the number problems is confusing.

All the letters represent variables or something that does not have a set value. The equation that the letters appear in merely shows the relationship between the two (or more) changing quantities.

The cartesian plane is just dots and lines, but it demonstrates a real-world application of math. Everything depends on something else, and the cartesian plane allows us to see that relationship with all the distracting noise stripped away.

C) Area, Volume, and The Fun Behind Shapes

The visual representation of any number squared is a square. The visual representation of any number cubed is a cube. That is either painfully obvious, or you just had your mind blown.

The real fun begins when you see it applied to other shapes.

There are some beautiful relationships between the 2 and 3-dimensional versions of shapes. The idea isn’t to memorize the exact relationships but to see that nearly every math idea has a real physical component that can help you grasp the underlying abstract concepts.

This makes learning math purposeful, and I always felt like understanding the physical ideas behind the numbers made it more fun and interesting. For more, read how to learn basic physic ideas.

Much of math becomes easier to study if you figure out the visual representations of an idea. Every topic you learn can be represented on the number line, the cartesian plane, or in the form of a shape.

6) A modern tip: Use technology to help your problem solving

With today’s technology, you can go extremely far without a teacher. Some tools will solve the problem for you when it comes to solving math problems. Unlike a simple calculator, these tools also walk you through each step.

These are fantastic for figuring out where you went wrong while also showing you how to solve the problem correctly.

I spent an entire year working on math problems from various books I downloaded, and nothing helped my math skills improve faster than running my work through one of these programs for feedback.

The three I recommend are:

1. Wolfram Alpha
2. Symbolab
3. Chegg Study

Regardless of which tool you select, remember what the purpose of using these types of problem solvers is:

You want to push yourself as hard as possible to solve the problem. You should check to see that your answer is correct only after you’ve given a decent effort. These tools are meant to assist your learning, not solve your problems. Unfortunately, many students learn lessons like this the hard way.

Checking the answer without pushing yourself to the limit of your knowledge and ability is no better than asking someone for the answer. If you use it this way, you never actually improve your problem-solving capabilities.

7) Be patient and work to get the concepts

The goal isn’t to be a human calculator or a math genius. It’s certainly not to memorize a bunch of different math problems.

Sadly, school trains you this way because they depend on funding, and it’s a lot easier to teach you to pass a test than learn.

The goal is to understand the concept. This is why you need to:

• Be patient
• Find great supplemental resources that provide simple explanations of complex ideas
• Take detailed notes
• Be willing to challenge your thought process

When I was working on my physics degree, I spent a lot of time on the site www.betterexplained.com. I even reached out to the site’s writer to thank him for all of his explanations. Another favorite site of mine was Paul’s Online Math Notes.

Both of these sites did a fantastic job explaining any new concepts I had trouble with and illuminating old mathematical concepts I never quite understood. They also both have unique approaches, which is extremely helpful for learning math.

In addition to the notes from their website, I also took a lot of notes and asked myself many questions. I forced myself to dig deep and truly grasp the material by asking myself questions.

There is nothing that facilitates learning more than asking the right questions.

A summary of the 7 tips to improve math skills

1. Believe that you can learn
2. Take your education into your own hands
3. Master the fundamentals of arithmetic
4. Learn to read math
5. Think in pictures
6. Use technology to help you learn
7. Take time to understand the concepts

If you work on solving problems and avoid memorizing everything but the basics, you will go far in whatever math courses you have to take. At the very least, you’ll be able to keep up with the students in any mathematics class.

The major lesson I learned from my journey is that you can learn anything given enough time.

This is the general strategy I used to go from a failing math student to getting a degree in physics. I believe that you can be a great math student with similar improvement if you follow these step-by-step instructions.